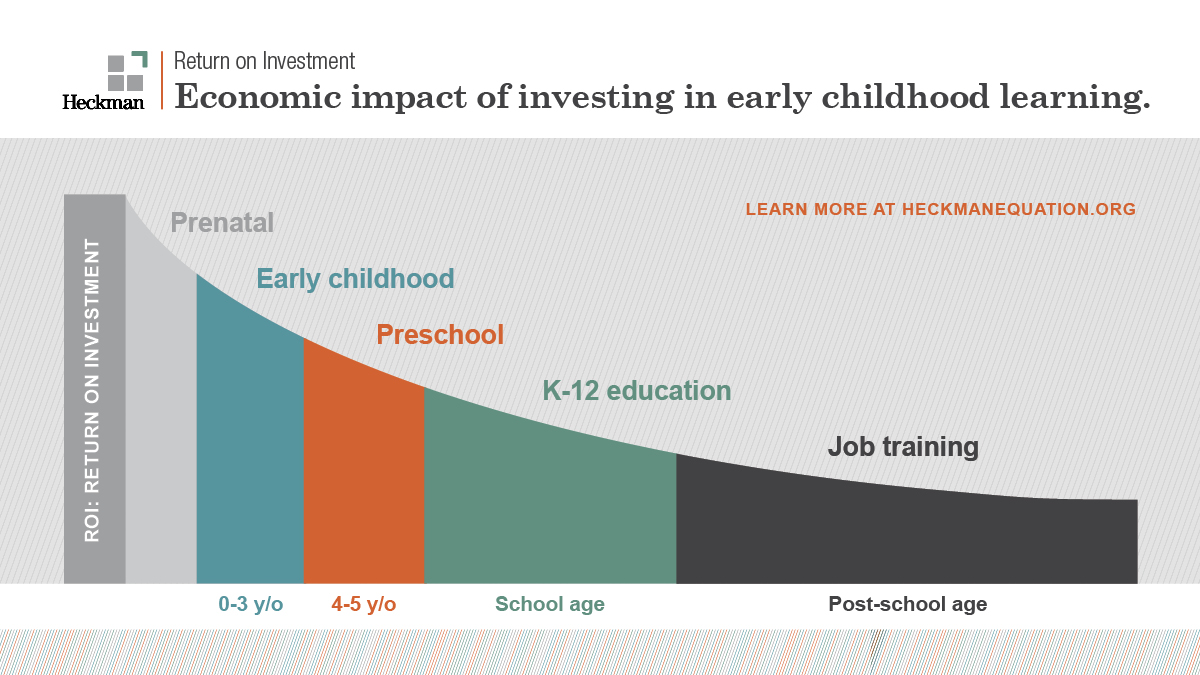
Die Heckman-Kurve ist ein wichtiges Konzept der Bildungsökonomie, benannt nach dem Nobelpreisträger für Wirtschaft, James Heckman. Diese Kurve veranschaulicht die wirtschaftliche Rendite von Investitionen in Bildung und Humankapital über die gesamte Lebensspanne eines Menschen. Kernaussagen der Heckman-Kurve sind:
- Frühzeitige Investitionen: Die Kurve zeigt, dass Investitionen in die frühkindliche Bildung und Entwicklung die höchste Rendite bringen. Das bedeutet, dass Geld, das in die Bildung und Förderung von Kleinkindern und Vorschulkindern investiert wird, langfristig den größten wirtschaftlichen und gesellschaftlichen Nutzen hat.
- Abnehmende Rendite: Mit zunehmendem Alter nimmt die Rendite von Bildungsinvestitionen ab. Das heißt, Investitionen in die Schulbildung haben immer noch einen positiven Effekt, aber nicht mehr so stark wie in der frühen Kindheit. Investitionen in Erwachsenenbildung oder berufliche Weiterbildung haben zwar immer noch einen positiven, aber vergleichsweise geringeren Effekt.
- Kumulative Effekte: Die Kurve betont auch, dass frühe Investitionen spätere Investitionen effizienter machen. Kinder, die früh gefördert werden, profitieren mehr von späteren Bildungsangeboten.
- Gesellschaftlicher Nutzen: Die Heckman-Kurve argumentiert, dass frühzeitige Bildungsinvestitionen nicht nur dem Individuum zugutekommen, sondern der gesamten Gesellschaft durch geringere Kriminalitätsraten, höhere Produktivität und geringere Sozialausgaben.
- Chancengleichheit: Ein wichtiger Aspekt der Kurve ist die Betonung der Bedeutung frühkindlicher Förderung für die Verringerung sozialer Ungleichheiten.
Trotz der Betonung frühkindlicher Bildung zeigt die Heckman-Kurve auch, dass Bildungsinvestitionen in jedem Lebensalter positive Effekte haben, auch wenn die Rendite mit zunehmendem Alter abnimmt. Sie ist ein starkes Argument für die Priorisierung frühkindlicher Bildung in der Bildungspolitik und für kontinuierliche Investitionen in das Humankapital über die gesamte Lebensspanne.
Literatur
https://heckmanequation.org/resource/the-heckman-curve/ (23-11-12)