Subitizing – Simultanerfassung. Online Lexikon für Psychologie & Pädagogik

Subitizing bzw. Simultanerfassung oder Ziffern-Modul bezeichnet die menschliche Fähigkeit, kleine Mengen von Objekten zu erkennen, ohne diese zählen zu müssen, wobei dieses intuitive Erfassen von Mengen bis vier offensichtlich einen angeborenen Aspekt der Wahrnehmung darstellt, während das Abzählen einer Menge über vier eine logische Fähigkeit darstellt, die erst erlernt werden muss (Stangl, 2020). Es wird auch angenommen, dass auf Subitizing die spätere Fähigkeit zum Zählen aufbaut.

In Studien mit Erwachsenen wurde festgestellt, dass die Quantifizierung von Mengen im Bereich von 1-4 schneller und mit höherer Richtigkeit erfolgt als bei Mengen zwischen 4 und 7. Dies deutet darauf hin, dass es zwei unterschiedliche Prozesse geben muss, die eine solche Quantifizierung erlauben, wobei der Bereich zwischen 4 und 5 der entscheidende Punkt zu sein scheint, bei dem ein Wechsel der Prozesse stattfindet, da hier eine Erhöhung der Antwortzeiten und eine höhere Fehlerquote auftreten. Bei Kindern ab 5 Jahren finden sich bis 4 Elemente fast keine Unterschiede in der Zeit und der Richtigkeit der Antworten beim Erkennen der Mengen, allerdings steigt die Antwortzeit ab 5 Elementen deutlich und auch die Fehlerquote ist höher.

Kutter et al. (2023) konnten nun zeigen, dass der Repräsentation von kleinen und großen Zahlen zwei getrennte neuronale Mechanismen zugrunde liegen, indem man Ableitungen einzelner Neuronen im medialen Temporallappen von neurochirurgischen Patienten durchgeführt hat, die Zahlen beurteilten, indem sie die Anzahl der Punkte auf einem Bildschirm schätzten, die eine halbe Sekunde präsentiert wurden. Man fand dabei eine Grenze in der neuronalen Kodierung um die Zahl 4, die mit dem Verhaltensübergang vom Subitieren zum Schätzen korreliert. Im Bereich des Subitierens zeigten die Neuronen eine überlegene Abstimmungsselektivität, begleitet von Suppressionseffekten, die auf eine Surround-Inhibition als selektivitätssteigernden Mechanismus schließen lassen. Im Gegensatz dazu nahm die Abstimmungsselektivität mit steigenden Zahlen jenseits von 4 ab, was ein verhältnisabhängiges Zahlenschätzungssystem charakterisiert. Offenbar gibt es im Gehirn Nervenzellen, die für bestimmte Anzahlen zuständig sind. Diese beiden Systeme und die sie trennende Kodierungsgrenze wurden auch mit Hilfe von Dekodierungs- und Clustering-Analysen ermittelt, wobei das identifizierte System zur Subitisierung kleiner Zahlen mit der Aufmerksamkeit und dem Arbeitsgedächtnis verbunden sein könnte, die vergleichbare Kapazitätsbeschränkungen aufweisen. Langfristig könnten diese Erkenntnisse zu einem besseren Verständnis der Dyskalkulie beitragen, einer Entwicklungsstörung, die durch mangelndes Zahlenverständnis gekennzeichnet ist.

Schon vor einigen Jahren konnte man zeigen, dass es im Gehirn Nervenzellen gibt, die für bestimmte Anzahlen zuständig sind, d. h., manche Neuronen feuern zum Beispiel vor allem bei Zweiermengen, andere bei Vierermengen und wieder andere bei Mengen von sieben Elementen. Allerdings sprechen die Neuronen auch auf leicht abweichende Anzahlen an, denn eine Siebener-Hirnzelle feuerte also auch bei sechs oder acht Elementen, dann aber schwächer, doch noch weniger lässt sie sich durch fünf oder neun Elemente aktivieren. Diesen Numerical Distance Effect wurde auch bei Primaten nachgewiesen. Interessanterweise scheint sich der Effekt beim Menschen aber nur bei höheren Anzahlen auszuwirken, denn für Mengen unterhalb von etwa fünf Elementen gibt es scheinbar einen zusätzlichen Verschaltungsmechanismus, der diese Neuronen präziser macht, denn wenn etwa eine Dreier-Hirnzelle feuert, hemmt sie dadurch gleichzeitig die Zweier- und Vierer-Hirnzellen, was das Risiko senkt, dass diese Zellen durch eine Dreiermenge fälschlicherweise miterregt werden. Bei Fünfer-, Sechser- oder Achter-Neuronen gibt es diesen Mechanismus hingegen nicht, sodass diese eine höhere Fehlerquote zeigen.

Zahlen sind für Menschen nach Butterworth (1999) konzeptionelle Werkzeuge, da sowohl die Wichtigkeit deren Gebrauchs, als auch die konventionellen Darstellungen kulturell abhängig sind. Dabei bedeutet der Ziffern-Modul die angeborene Fähigkeit von Menschen, Mengen im Bereich von 0 bis 4 oder 5 zu unterscheiden, wobei diese Fähigkeiten auch Tiere wie Tauben und Ratten besitzen. Schon fünf Monate alte Kinder sind in der Lage, den Unterschied zwischen Mengen von Gegenständen im Bereich von 1 bis 4 zu erkennen, d. h., sie erkennen visuell, ob eine Menge größer oder kleiner als die andere ist und haben auch einen angeborenen Sinn, um nicht logische Additionen oder Subtraktionen zu identifizieren. Bei diesem Bereich handelt es sich um ein holistisches Erkennens von Mengen. Nach Ansicht mancher Experten kann durch gezieltes Training diese Fähigkeit auf acht und mehr Objekte gesteigert werden, jedoch ist ungeklärt, ob es sich dabei tatsächlich noch um eine Simultanwahrnehmung handelt, oder ob es sich nicht eher um das Erkennen von strukturierten Mehrfachanordnungen handelt. Diese Fähigkeit des Menschen schnell im visuellen Bereich Gruppen von Gegenständen zu bilden, hilft ihm auch eine größere Menge in kleinere Einheiten zu zerlegen und so eine Aufgabe schneller zu lösen. So kann man etwa beim Zählen von 18 Gegenständen schneller vorankommen, wenn man die Menge in Einheiten zu drei aufteilt und dann die Anzahl der Gruppen mit dem Inhalt multipliziert.

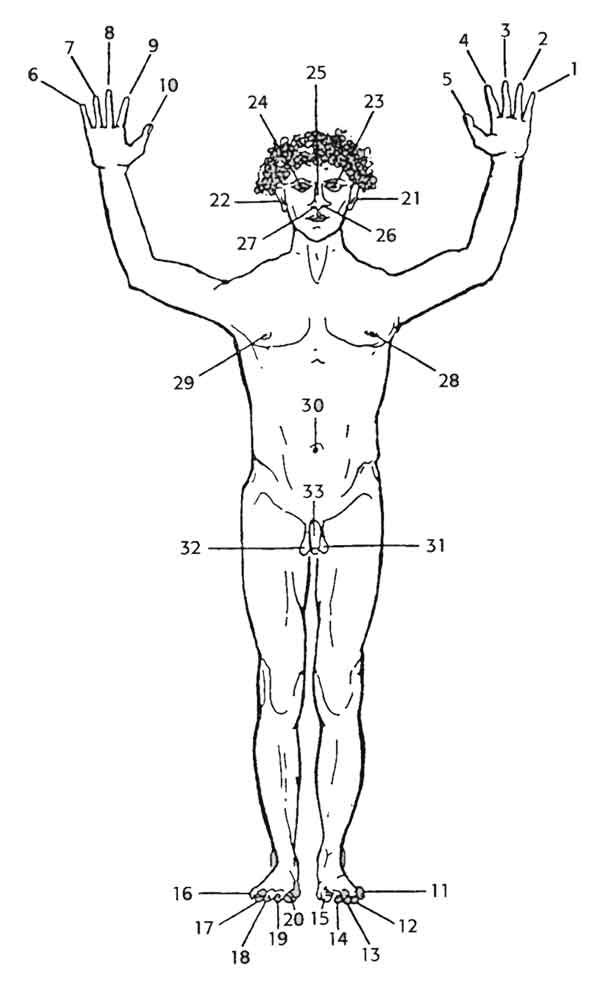In vielen Kulturen werden Zahlen durch Körperteile dargestellt, wobei in der westlichen Kultur meist die Finger benutzt werden, um Mengen anzuzeigen, wobei die dargestellte Anzahl von Fingern für die identische Anzahl an Gegenständen steht. Allerdings ist die Darstellung der Zahlen mit Fingern kulturell abhängig, denn die Zahl „zwei“ kann z. B. durch den Zeigefinger und den Mittelfinger dargestellt werden, oder aber durch den Daumen und den Zeigefinger. In China dagegen bedeutet diese letztere Darstellungsform entweder 7 oder 8, je nachdem ob die Finger nach unten oder nach oben zeigen. Es gibt übrigens Völker, wie die Yupno Menschen aus Papua Neu-Guinea, die keine spezifischen Wörter für Zahlen kennen, denn sie benutzen ihre Körperteile, um Mengen zu quantifizieren, sodass die einzelnen Körperteile synonym für Zahlen stehen.

Zählen unterscheidet sich vom Subitizing dadurch, dass hier nicht mehr die ganzheitliche Wahrnehmung einer Menge aktiviert wird, sondern dass es darum geht, eine Anzahl durch Eins-zu-eins Zuordnung zu gliedern, und jeder Zuordnung einen kulturell abhängigen Zahlencode zu geben, wobei der letzte Zahlencode dann die Gesamtanzahl der Menge bezeichnet. Zählen ordnet somit Mengen und dient dem genauen Feststellen von u. a. Mengen, Größen, die größer sind als der Subitizing-Bereich. Das Zählen entwickelt sich bei Kindern dabei nach folgenden Prinzipien: Zuerst zählt ein Kind jeden Gegenstand einzeln und gibt den Gegenständen auch immer die gleiche Wertigkeit, worauf die stabile Reihenfolge folgt, bei der es unwichtig ist, ob das Zählen korrekt abläuft, denn das Kind benutzt immer die gleiche Reihenfolge mit den gleichen Fehlern, etwa „eins, zwei, vier, sieben. Als letzte Stufe gilt die Kardinalität, bei der die benutzte Zahlenreihe korrekt ist und das Kind verstanden hat, dass das zuletzt benutzte Wort der Wertigkeit dieser Menge entspricht. Als Voraussetzung für das Zählen gelten dabei das Abstraktionsprinzip, d. h., die benutzten Zahlen sind unabhängig vom gezählten Gegenstand, und die Anordnungsbeliebigkeit, d. h., dass die Reihenfolge der Gegenständen beim Zählen Auswirkung auf das Ergebnis hat.

Übrigens ist eine defizitäre Simultanwahrnehmung keine belegbare Ursache für eine Dyskalkulie (Rechenschwäche), denn gezielte Trainings führen zwar zu erhöhten Trefferquoten, ohne dass dabei aber irgendein begriffliches Lernen in Bezug auf Mengen oder Zahlen stattfindet. Eine schlechte Simultanwahrnehmung findet sich auch bei Kindern mit gutem mathematischem Verständnis.

Literatur

Butterworth, B. (1999). What counts: how every brain is hardwired for math. New York: Free Press.
Kutter, Esther, F., Dehnen, Gert, Borger, Valeri, Surges, Rainer, Mormann, Florian & Nieder, Andreas (2023). Distinct neuronal representation of small and large numbers in the human medial temporal lobe. Nature Human Behaviour, doi:10.1038/s41562-023-01709-3.
Stangl, W. (2001). Stufen der sensumotorischen Intelligenz. [werner stangl]s arbeitsblätter.
WWW: https://arbeitsblaetter.stangl-taller.at/KOGNITIVEENTWICKLUNG/Sensomotorik.shtml (01-05-23)
Stangl, W. (2023, 7. Oktober). Schätzen oder Subitieren? – Psychologie-News.
https:// psychologie-news.stangl.eu/4734/schaetzen-oder-subitieren.
Wantz, M. (2008). Zahlen und Psychomotorik. motorik’. Zeitschrift für Motopädagogik und Mototherapie, 31, 82-89.
https://de.wikipedia.org/wiki/Simultanerfassung (19-12-12)